pschlik, on 02 August 2023 - 07:16 PM, said:
pschlik, on 02 August 2023 - 07:16 PM, said:
So, running things through the debugger, I found that this is caused by the way curve resistance is compensated for based on speed, which in turn is affected by how superelevation (as in, the under-the-hood superelevation, not the 3D dynatrax superelevation) is set up. In the ROUTES\SP_Shasta\OpenRails folder, we find the OpenRails extension of SP_Shasta.trk, which includes the superelevation profile used on this route.
ORTSTrackSuperElevation ( 0 0.000 100 0.000 120 0.070 150 0.08 167 0.089 175 0.083 184 0.083 194 0.089 874 0.089 1166 0.0635 1749 0.044 3497 0.0254 6994 0.019 10000 0 )
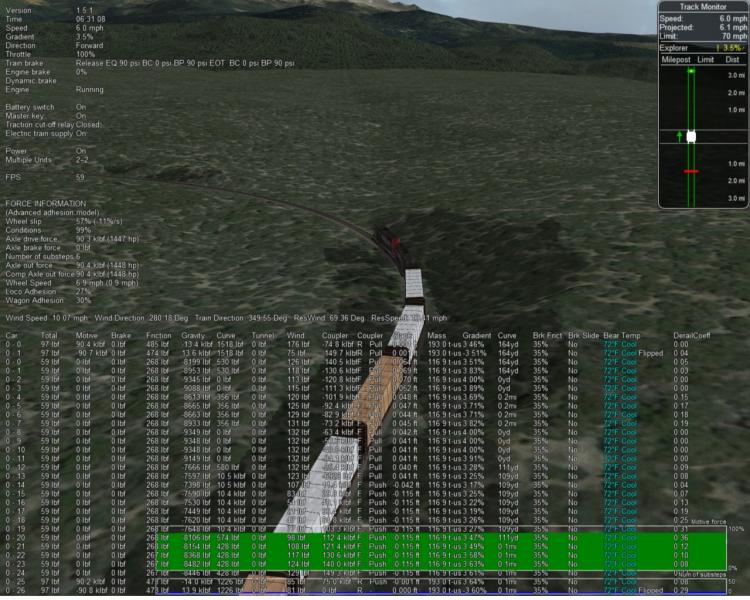
The thing to observe here is that second pair of numbers: 100, 0.000...any track with a radius of less than 100 meters will be simulated as having 0 meters of superelevation. This sounds reasonable and innocent, but the speed modification part of the curve resistance code would calculate an ideal speed of 0 when there's no superelevation (this is accurate), which would then cause division by 0, setting curve resistance to a nonreal (infinite) value (which we obviously don't want). So superelevation is clamped to no less than 0.0001...which means that instead of getting an ideal speed of 0, you get an ideal speed of something tiny like 0.5 mph. So division by 0 is solved and replaced by division by...a small number close to 0. Great, the resistance isn't multiplied by infinity, but it is multiplied by 20 or so...and you end up with the problem found here.
Clearly, the formula used isn't very accurate. I understand this is meant to estimate how deviating from the ideal speed increases centripetal or centrifugal forces which would in turn increase flange friction, but it's been simplified too far and cannot handle perfectly reasonable 'edge' cases. I wonder if there's more research material out there on better compensation factors to replace the linear one used by OR.
The much more swift and practical remedy is to change the superelevation profile to this:
ORTSTrackSuperElevation ( 0 0.005 100 0.010 120 0.070 150 0.08 167 0.089 175 0.083 184 0.083 194 0.089 874 0.089 1166 0.0635 1749 0.044 3497 0.0254 6994 0.019 10000 0 )
This would be similar to the way Mullan's superelevation profile was set up: Setting the 100 meter radius superelevation to 0.010 meters changes the calculated ideal speed for the 100 meter curve from about 0.5 mph to around 5 mph, which is enough to avoid the explosion in force (resistance is closer to 1,000 pounds than 10,000).
Fun fact: Driving through a curve that OR calculated to have an ideal speed of 0.5 mph at a speed of 10 mph will have the same curve resistance as driving through a curve with a 50 mph ideal speed at 1000 mph! All OR sees is that you are going 20x the ideal speed, completely ignoring the fact that one case is going above the ideal speed by just 10 mph, and the other is going above the ideal speed by 950 mph.
Thank you very much for that detailed analysis, including taking the time to look into the Superelevation profile for Shasta. 🙂
I did some additional investigation after your comment, and I now fear that the entire curve resistance model for ORTS is gravely flawed. I first modified the Superelevation profile for Shasta to have 0.01905 meters (3/4") of super at 0 radius and 100 radius. This resulted in the "balancing speed" for my SD40-2 test model landing around 8 MPH (seems fairly reasonable). I noticed that when I am at that equilibrium speed, curve resistance drops to literally zero pounds on my SD40-2. That is absolutely wrong, as it contradicts all literature I have read on the subject (including literature in the Open Rails manual itself). With the current ORTS code, you can be traveling through an extremely tight curve, but as long as you traveling at "equilibrium speed" you have zero curve force, which makes no physical sense. While it is true that there is no force towards the inside of the curve or the outside of the curve related to weight/centripetal force specifically when traveling at the equilibrium speed, there should still be curve resistance due to the rigid wheelbase itself and the angle of attack of the leading and trailing wheels of every bogie digging into the rails, causing increased friction the tighter the curve is.
In other words, curve resistance is supposed to have TWO components - the one that is normally thought of is related to the angle of attack of the wheels (proportional to length of the rigid wheelbase), and the other more minor component would be related to how far above or below equilibrium speed you are, which adds an *additional* friction force on top of the base curve resistance caused by the rigid wheelbase/angle of attack effect (I have read some literature indicating minimum curve force may actually occur at a slight cant excess rather than true equilibrium).
This would be great to get Peter Newell roped in on. His derailment force calculation code with wheel climb, etc. may have some good knowledge cross-over that we can apply.
AREMA's standard formula is 0.8 lb/ton per degree of curve for a 2 axle truck but obviously that is simplified, and it's not clear if that factor assumes equilibrium speed let alone details on rigid wheelbase (more likely superelevation is not considered at all because it is such a minor factor)
Long story short, although I now have a solution to avoid the bizarre excessively high curve force, it seems like the curve resistance model really needs a complete overhaul regardless. My initial impression is that the most prudent thing would be to follow AREMA precedence and use the 0.8 lb/ton/degree of curve factor for 2 axle trucks as the start point and not even consider superelevation until some reliablebinfo can be found to indicate whether it has a significant enough effect for us to worry about.
Generally superelevation design is driven by safety factors (derailment prevention) and comfort factors. It's important to realize that for a train at a particular speed on a particular curve, at a speed below equilibrium, although the excess superelevation causes extra loading on the low rail, in turn it is also causing diminished loading on the high rail. Vice versa, if there is deficient superelevation, the high rail is getting loaded more, but weight is being taken off the low rail. These factors can cause excessive rail wear or plastic deformation on ONE of the rails, but I would expect the *net* increase in curve resistance to be very minor.

 Log In
Log In Register Now!
Register Now! Help
Help